Mapping a texture on a disc

When you're using openGL and mapping a texture on a plain basic quad it is a quite trivial task. Though when the quad (two triangles) has a bit more tropical shape, it's not so obvious anymore. I ran into this problem when trying to map a texture onto a 2d disc. The shape onto which I wanted to map a texture looks like this:

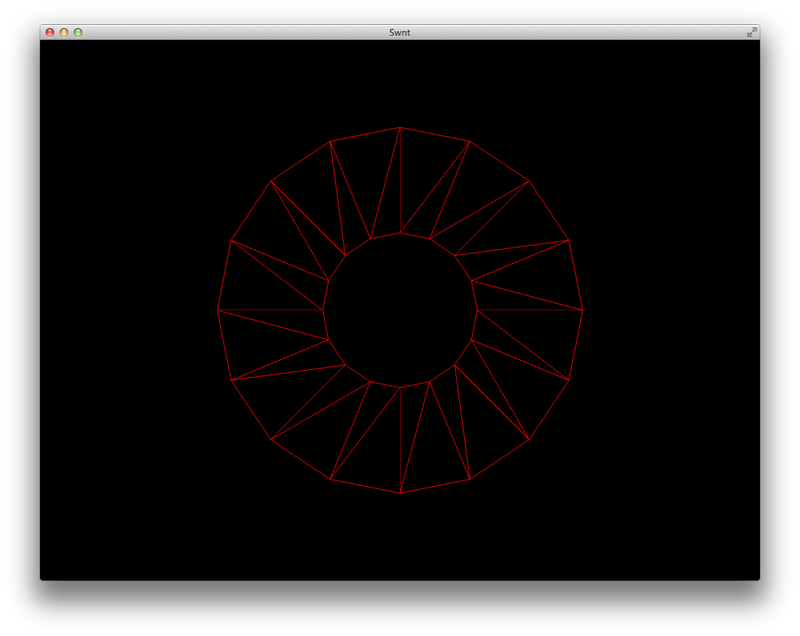
When looking at this image it's directly obvious that the triangles are not nicely spread out over the disc and that the widths of the quads are different, when comparing the inner and outer segments.

When you map a texture onto a shape like this it will result in something like shown in the image below. Notice how much the texture gets distorted and you can clearly see the triangles.

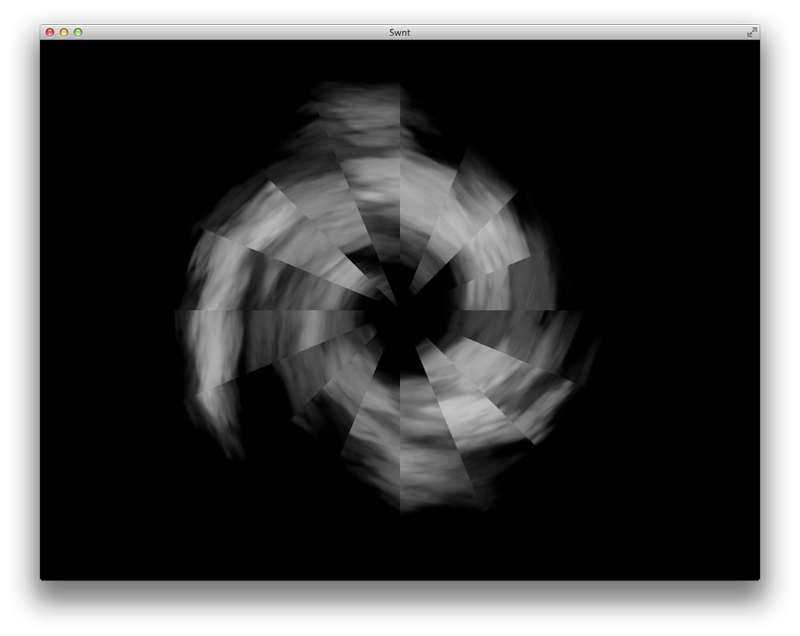
Luckily there is a solution for this! The solution is similar to the way we do projective interpolation and is described in great detail on this page..

In short the solution to this, is to add a 3rd texture coordinate which is used to scale the interpolation. We call this extra texture coordinate q. The algorithms works like:

• Get the intersection point of the two diagonals of the quad
• Get the distance to this intersection point for each of the 4 points that make the quad
• Scale the texture coordinates according the formula as provided by the above link

On the CPU we calculate the q values (see linked post) and store those in a vertex attribute. Then we use this q value in the fragment shader to scale the texture coordinate.

Calculate the q (and vertices of the ring)

The code below is a bit verbose to clarify the steps we take to calculate the q value. See below for a more concise example.

void Mist::createRing(float x, float y, float radius, float width) {
  offsets.push_back(vertices.size());
 
  float resolution = 16.0;
  float angle = TWO_PI/resolution;
  float outer_radius = radius + width;
 
  for(int i = 0; i < resolution; ++i) {
    float c0 = cos( (i + 0) * angle);
    float s0 = sin( (i + 0) * angle);
    float c1 = cos( (i + 1) * angle);
    float s1 = sin( (i + 1) * angle);
 
    // positions
    vec3 pa(c0 * radius, s0 * radius, 0.0f);
    vec3 pb(c1 * radius, s1 * radius, 0.0f);
    vec3 pc(c1 * outer_radius, s1 * outer_radius, 0.0f);
    vec3 pd(c0 * outer_radius, s0 * outer_radius, 0.0f);
 
    // texcoords
    float u0 = float(i+0)/resolution;
    float u1 = float(i+1)/resolution;
    vec3 ta(u0, 0.0f, 1.0f);
    vec3 tb(u1, 0.0f, 1.0f);
    vec3 tc(u1, 1.0f, 1.0f);
    vec3 td(u0, 1.0f, 1.0f);
 
    // calculate distances from the corners to the centers
    vec3 intersection;
    if(!intersect(pa, pc, pb, pd, intersection)) {
      printf("The vertices of the dist do not intersect. Error.\n");
      ::exit(EXIT_FAILURE);
    }
 
    float d0 = length(pa - intersection);
    float d1 = length(pb - intersection);
    float d2 = length(pc - intersection);
    float d3 = length(pd - intersection);
 
    ta = ta * ((d0 + d2)/d2);
    tb = tb * ((d1 + d3)/d3);
    tc = tc * ((d2 + d0)/d0);
    td = td * ((d3 + d1)/d1);
 
    // store the vertices
    VertexPT3 a(pa,ta);
    VertexPT3 b(pb,tb);
    VertexPT3 c(pc,tc);
    VertexPT3 d(pd,td);
 
    vertices.push_back(a);
    vertices.push_back(b);
    vertices.push_back(c);
    vertices.push_back(a);
    vertices.push_back(c);
    vertices.push_back(d);
  }
 
  counts.push_back(vertices.size()-offsets.back());
  needs_update = true;
}

Another, shorter version of this was provided by Victor Martins:

// From: http://www.reedbeta.com/blog/2012/05/26/quadrilateral-interpolation-part-1/
float off = fabsf(sinf(time*0.5f))*130.0f;
float3 verts[4];
float3 uvs[4];
float vertDistanceToCenter[4];
 
uvs[0].set( 0, 0, 1 );
uvs[1].set( 1, 0, 1 );
uvs[2].set( 1, 1, 1 );
uvs[3].set( 0, 1, 1 );
 
verts[0].set( 100, 100, 1 );
verts[1].set( 500, 100+off, 1 );
verts[2].set( 500, 500-off, 1 );
verts[3].set( 100, 500, 1 );
 
Segment s1( verts[0], verts[2] );
Segment s2( verts[1], verts[3] );
 
float3 intersectPoint = IntersectionLineLine2D( s1.p0, s1.p1, s2.p0, s2.p1 );
for( int i=0; i<4; i++ ) {
    float dist = (intersectPoint - verts[i]).length();
    vertDistanceToCenter[i] = dist;
}
for( int i=0; i<4; i++ ) {
    int i2 = (i+2) % 4;
    uvs[i] = uvs[i] * ( (vertDistanceToCenter[i] + vertDistanceToCenter[i2]) / vertDistanceToCenter[i2] );
}

Then in the shader we scale the texture coordinate:

// GLSL
vec4 diffuse_color = texture(u_tex, v_tex.xy / v_tex.z);

The result is a lot better.